题目描述
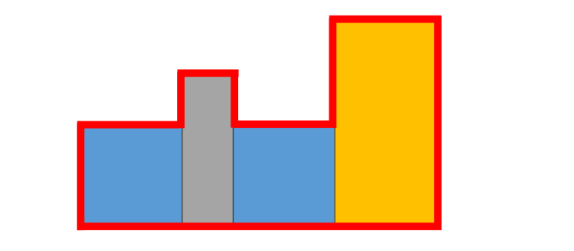
李明将 N 个矩形依次从左到右摆放成一排,相邻的矩形之间紧密贴合。李明想要知道拼合成的图形的外部周长,“外部周长”如下图红线部分所示。李明还想进一步知道,对于每一个 k=1,2...,N,当她从左到右摆放完前 k 个矩形时,此时的外部周长是多少。
输入格式
输入文件的第一行是两个正整数 N,Q;
其中 N为矩形的总数,Q 为输入文件的特征标号(含义见下文“数据规模与其他约束”部分);
输入文件的之后 N 行,每行两个正整数 ai,hi;
其中 ai 表示第 i 个矩形与地面接触的长度,hi 表示第 i 个矩形的高。
输出格式
输出共 N 行,其中第 k 行为一个正整数,表示从左到右摆放至前 k 个矩形后,此时图形的外部周长。
样例输入
4 0
2 2
1 3
2 2
2 4
样例输出
8
12
16
24
说明
数据范围
每个输入文件有一个特征标号 Q,用于标注本次输入的一些特殊性质:
- Q=1 表示矩形高度单调递增,任取两个相邻的矩形,后一个的高度大于等于前一个的高度。即 hi+1≥hi,i=1,...,N−1;
- Q=2 表示矩形高度单调递减,任取两个相邻的矩形,后一个的高度小于等于前一个的高度。即 hi+1≤hi,i=1,...,N−1;
- Q=0 表示无特殊性质。
所有数据均满足:
1≤ai,hi≤N,
Q 保证为 0、1、2 三者之一。
测试文件的分布如下表:
| 占比 |
N |
数据范围 |
| 40% |
1≤N≤10 |
1/2 满足 Q=1 |
| 30% |
1≤N≤1000 |
1/3 满足 Q=1 另外 1/3 满足 Q=2 |
| 30% |
1≤N≤105 |
1/3 满足 Q=1 另外 1/3 满足 Q=2 |

