题目描述

给定一棵以 $1$ 为根的有根树，树的顶点编号为 $1,2,\dots,N$。对于每个顶点 $i$ （$2\le i\le N$），它的父亲是顶点 $p_i$（且 $1\le p_i<i$）。初始时所有顶点均为白色。

你可以重复执行如下操作（次数为非负整数）：

• 选择一对整数 $(u,v)$ 满足：

  • $1\le u<v\le N$；
  • 顶点 $u$ 与顶点 $v$ 当前均为白色；
  • 顶点 $u$ 不是顶点 $v$ 的祖先（即从 $v$ 沿着父边不断向上无法到达 $u$）。

• 将顶点 $u$ 与顶点 $v$ 颜色同时改为黑色。

在恰当的操作顺序下，问最多可以执行多少次这样的操作？（即求最多能染黑的白色顶点对数）

你需要对 $T$ 个测试用例分别求解。

输入格式

第一行包含一个整数 $T$，表示测试用例数。

接下来对每个测试用例依次给出：

• 第一行包含一个整数 $N$；
• 第二行包含 $N-1$ 个整数 $p_2,p_3,\dots,p_N$，其中对每个 $i$（$2\le i\le N$）满足 $1\le p_i<i$。

所有测试用例的 $N$ 之和不超过 $5\times 10^5$。

输出格式

输出 $T$ 行，第 $i$ 行为第 $i$ 个测试用例的答案（一个整数），表示最多可以执行的操作次数。

样例输入

4
6
1 2 2 2 5
7
1 2 3 4 5 6
7
1 2 3 4 2 4
12
1 1 2 2 2 4 4 4 7 7 7

样例输出

2
0
2
5

说明

样例解释

对于第一个测试用例，

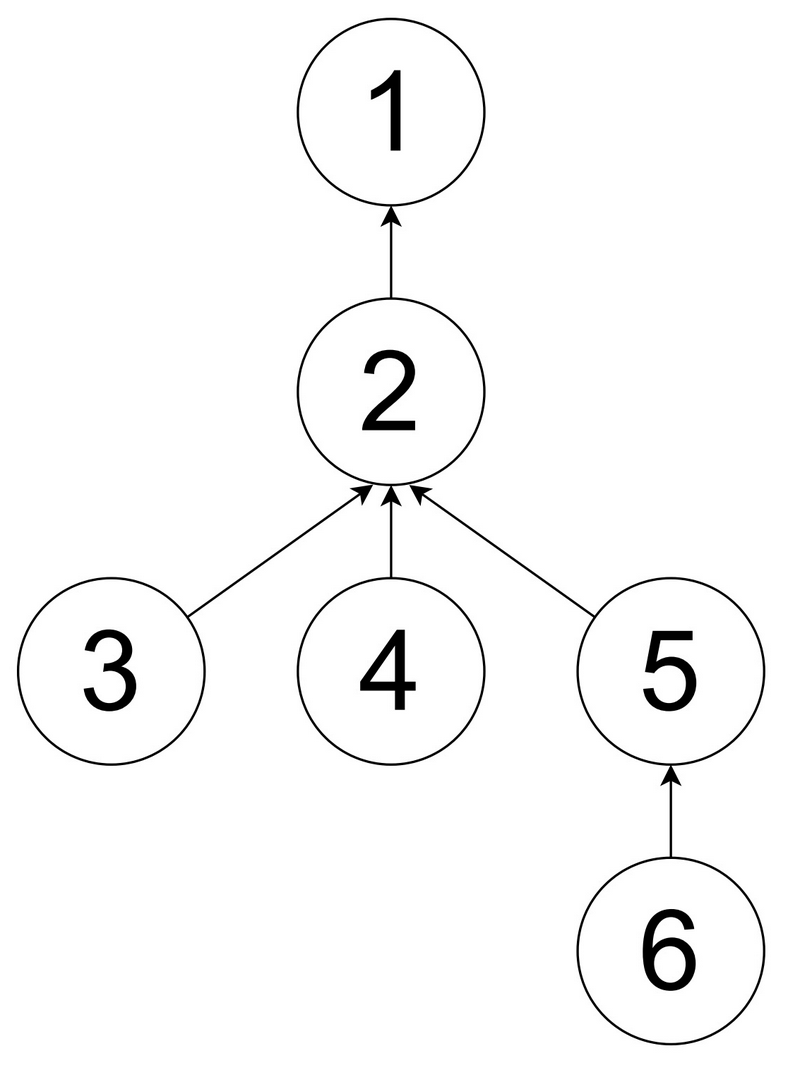
一个可行的两次操作为：

• 选择 $(u,v)=(3,5)$，将顶点 $3,5$ 变为黑色。
• 选择 $(u,v)=(4,6)$，将顶点 $4,6$ 变为黑色。

不能再执行更多操作，因此答案为 $2$。

数据范围

• $1\le T\le 5\times 10^4$；
• $2\le N\le 5\times 10^5$；
• $\sum N$（所有测试用例）$\le 5\times 10^5$；
• $1\le p_i<i$ 且均为整数。